การรู้จักคนิตศาสตร์

4. การหารพหุนาม

การหารพหุนามของตัวแปร x ที่มีดีกรีมากกว่าหรือเท่ากับ 1 ด้วยพหุนามที่อยู่ในรูป x - a เมื่อ a 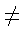 0 เช่น

ด้วยวิธีการหารยาวเราสามารถหาผลหารได้ดังนี้

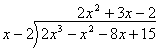ดังนั้น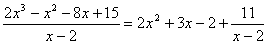 

วิธีการหารยาวดังกล่าว ค่อนข้างจะเสียเวลา การหารสังเคราะห์เป็นวิธีลัดในการหาผลหารและหาเศษจากการหาร จากตัวอย่างข้างต้นที่กล่าวไปแล้ว จะพบว่ามีตัวเลขบางตัวเกิดซ้ำเช่น 2 , 3 และ -2 ซึ่งเป็นสัมประสิทธิ์ของผลหาร จะเกิดขึ้นในระหว่างการหารสามครั้งและตัวเลข -8 , 15 ซึ่งเป็นสัมประสิทธิ์ของสองพจน์สุดท้ายของตัวตั้งเกิดซ้ำในระหว่างการหารสองครั้ง ถ้าเรานำกระบวนการหารยาวดังกล่าวมาเขียนใหม่อยู่ในรูปสามแถว ดังนี้

		แถวที่ 1
		แถวที่ 2
		แถวที่ 3

จากการสังเกตจะพบว่า จำนวนแต่ละจำนวนในแถวที่ 2 เกิดจากการนำ -2 คูณกับจำนวนที่มาก่อนของแถวที่ 3 เช่น

-4 เกิดจาก การนำ -2 คูณกับ 2

-6 เกิดจาก การนำ -2 คูณกับ 3

4 เกิดจาก การนำ -2 คูณกับ -2

นอกจากนั้น จำนวนแต่ละจำนวนในแถวที่สาม ( ยกเว้นจำนวนแรก ) เกิดจากผลต่างระหว่างจำนวนในแถวที่ 1 และแถวที่ 2 ที่อยู่ในตำแหน่งเดียวกัน เช่น

-3 เกิดจาก -1 – (- 4)

-2 เกิดจาก -8 – (- 6)

11 เกิดจาก 15 – 4

ตัวอย่างที่ 4. จงหา   วิธีทำ ในที่นี้ x - a = x – 3 ดังนั้น a = 3 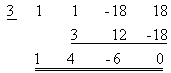                         ดังนั้น =  หรือ  =  ในตัวอย่างนี้ เศษจากการหารเท่ากับ 0 แสดงว่าหารลงตัว

-->x = poly(0,'x'); -->s =x^3+x^2-18*x+18 s =       18 - 18x + x2 + x3 -->t =x-3 t =       - 3 + x -->[n,d] = pdiv(s,t)         // คำสั่งที่ใช้หาร d =                      // จำนวนเต็มที่ได้จากการหาร       - 6 + 4x + x2 n =                     // เศษที่ได้จาการหาร      0.

ตัวอย่างที่ 5. จงหา  วิธีทำ ในที่นี้ x – a = x + 1 = x – (-1) ดังนั้น a = -1 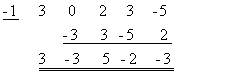             ดังนั้น  หรือ

-->x = poly(0,'x'); -->s = 3*x^4 + 2*x^2 + 3*x - 5 s =      - 5 + 3x + 2x2 + 3x4 -->t = x+1 t =      1 + x -->[n,d] = pdiv(s,t) d =                  // จำนวนเต็มทีได้จากการหาร      - 2 + 5x - 3x2 + 3x3 n =                  // เศษที่ได้จากการหาร      - 3.