รากที่สองในระบบจำนวนจริง
บทนิยามรากที่สองของ 
ตัวอย่าง เช่น
1.  ดังนั้น
ดังนั้น 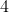 เป็นรากที่สองของ
เป็นรากที่สองของ 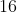
2.  ดังนั้น
ดังนั้น 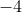 เป็นรากที่สองของ
เป็นรากที่สองของ 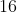
3.  ดังนั้น
ดังนั้น 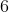 เป็นรากที่สองของ
เป็นรากที่สองของ 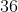
4.  ดังนั้น
ดังนั้น 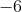 เป็นรากที่สองของ
เป็นรากที่สองของ 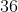
5.  ดังนั้น
ดังนั้น  เป็นรากที่สองของ
เป็นรากที่สองของ 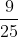
6.  ดังนั้น
ดังนั้น 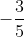 เป็นรากที่สองของ
เป็นรากที่สองของ 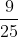
จากตัวอย่่างข้างต้นจะเห็นได้ว่า ค่าของรากที่สองของ จำนวนจริงใดๆที่มีค่ามากกว่าหรือเท่ากับศูนย์ มีสองค่า คือ
-ค่าที่เป็นบวก และ
-ค่าที่เป็นลบ
เช่น รากที่สองของ 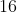 มีสองค่า คือ
มีสองค่า คือ 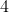 และ
และ 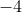
รากที่สองของ 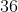 มีสองค่า คือ
มีสองค่า คือ 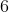 และ
และ 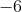
ตัวอย่างที่ 1 จงหารากที่สองของ
1) 
หารากที่สองของ  พูดง่ายๆก็คือหาว่าเลขอะไรเอ๋ย ยกกำลังสองแล้วได้
พูดง่ายๆก็คือหาว่าเลขอะไรเอ๋ย ยกกำลังสองแล้วได้ 
นั่นก็คือ 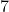 และ
และ 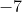
2) 
เนื่องจาก  และ
และ 
ดังนั้นรากที่สองของ 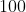 คือ
คือ 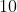 และ
และ 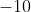
3) 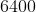
เนื่องจาก  และ
และ 
ดังนั้นรากที่สองของ 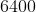 คือ
คือ 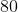 และ
และ 
บทนิยาม ของ 
ตัวอย่างจงหาค่าต่อไปนี้
1.
2.
3.
4.
5.


ไม่มีความคิดเห็น:
แสดงความคิดเห็น